【統計一口メモ　第26話】例数設計―ｎ数と検出力―

名古屋市立大学大学院医学研究科 非常勤講師　薬学博士　松本一彦

よく知られているように、検定ではサンプル数（ｎ数）が大きくなればなるほど、　よりわずかな差で有意になります。反対にｎ数が少なすぎて本当は差があるにもかかわらず検定では有意差がみられないこともよく経験します。

ガイドラインにしたがった毒性試験では、ｎ数は決まっていて例数設計の出番はありませんが、薬理試験や探索毒性試験では、しばしば例数設計の問題が出て来ます。

§１．「例数設計でN数を求めているが，“検出力”が出ていない。検出力とｐ値を併記せよ」　と言われたら？

本来、例数設計は本試験で必要な例数を予備試験のデータから算出する時に必要になります。予備試験で例数設計をするには，次の式を用います。

必要なデータは、“2群の平均値と標準偏差”です。

ZはNORMSINV関数で求めます。βは検出力(1-β）を求めるために使いますが、通常は0.2です。ＳＤは両群の標準偏差の平均値です。Δ（デルタ）は平均値の差です。

Zα/2とZβは、それぞれ正規分布の上側α/2％点とβ％点を表しています（両側検定）。

α=0.05、β=0.2とします。

Z_0.025＝NORMSINV(1-0.025)＝1.96　　Ｚ_0.20＝NORMSINV(1-0.2)＝0.84　を用います。

実際の計算に入る前に検出力“1-β”について復習しておきましょう。

§２．＜２つの過誤と検出力＞

第1種の過誤：2群間に薬効あるいは毒性の差がないにもかかわらず、差があるという判断を下してしまうこと（αの過誤、あわてものの過誤）。通常は５％を用います。

第２種の過誤：群間に薬効あるいは毒性の差があるにもかかわらず、差がないという判断を下してしまうこと（βの過誤、ぼんやりものの過誤）。通常は２０％を用います。

検出力とは１－βで、有意差が見つかる確率です。通常８０%が用いられます。

§３．「例題：1群あたり５頭の高血圧犬を用いて、対照群に対する薬剤の降圧効果を調べた。α=0.05（両側）、β=0.20の条件で例数設計を行うと1群あたり必要な例数は何例になるだろうか？」　

浜田知久馬（興交易出版部）一部改変^１）

α=0.05、β=0.2、SD＝(14.4+16.6)/2=15.5、 Δ＝177―161.8＝15.2

　　　　　　N＝２｛Z_α/2＋Z_β｝²SD²/Δ²

　　　　　　＝２x(1.96+0.84)²x15.5²/15.2²＝16.3

必要例数=17

§４．Pharmaco Basicでの＜例数設計＞

平均、標準偏差、N数を入力します。

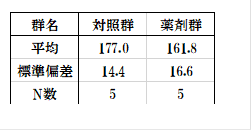
例題の予備試験5例の結果はp=0.1605で有意差なし、検出力＝0.341

そこで、５例をスタートに有意差（緑）が出るまでｎ数を増やしてみます。

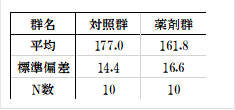
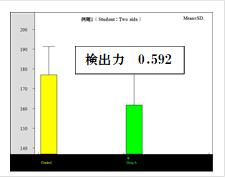
10例で有意差がみられた（ｐ=0.042）のですが、検出力は0.592で0.8には届きませんでした。

そこで、さらにｎ数を増やして検出力が0.8を超すには何例いるかをみました。

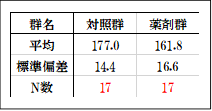
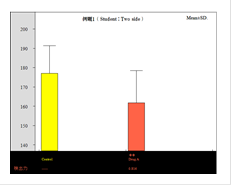
検出力が0.8を超えるには、n=17必要でした。

§５．例数設計へのもう一つのアプローチ　＜例数を減らすくふう＞

例題ではｎ数が17必要になったわけですが、高血圧犬でその数を揃えることは難しい。そのような場合どうすればいいのだろうか？　例数設計に必要なものは“平均値の差Δ”と“標準偏差の平均値”でした。そこで、まず動物の体重や年齢を揃えて、バラツキを小さくすることを考えます。その次に、もっと効果の高い薬剤に変えることでΔを大きくすることです。

まず、両群のバラツキを小さくしてみましょう。両群とも標準偏差を20%小さくしたときは、検出力0.820でN数が11となりました。バラツキはそのままで、薬剤の効果がより高いものを使ってもN数の減少につながります。この例でも薬剤群の効果を10%強くするとN数は７となりました。

標準偏差を小さく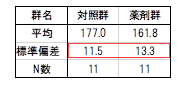

平均値の差を大きく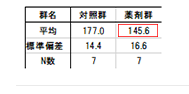

※ボクのつぶやき：探索的段階にあれば薬剤群でより効果の強いものを選ぶこともできるけど、1つに絞った後は難しい。その時はバラツキを小さくするしかないなー。動物実験であれば実験条件を慎重に整えること、臨床試験であれば無作為抽出する母体の吟味をしっかりせねば。それにしてもΔを大きくする方がｎ数減少に効くなー。

§６．例数設計についての一統計家の言葉

「サンプル数が巨大ならばほとんどが検定を通る」のが問題だとすれば、その原因はサンプル数そのものではなく検定が基づいている判断基準の方に求めるべきではないか。「適切なサンプル数にせよ」というアドバイスは、その点ではミスリーディングである(佐藤俊樹)^２）。

※ボクのつぶやき：社会学や臨床とは異なり実験が主体の生物統計の世界では“巨大”はあり得ない。確かに巨大であれば検定は必要ないのかもしれない。でも少数例を扱うボクたちにはやっぱ「適切なサンプル数」は必要なアドバイスなんだなー。ただ、先の統計家も検定はいらないとは言ってなかった。「―――統計学的検証は判断材料の一つにすぎない。理論的な美しさや価値観、外部データとの整合性などを総合的に判断をして、何を正しいと主張するか決めるしかない」と締めくくっていた。

• 1）浜田　知久馬「新版学会・論文発表のための統計学」真興交易（株）医書出版部　2016年
• 2）佐伯　胖、松原　望　編「実践としての統計学」東京大学出版会　2000年
• Pharmaco 工房：https:pharmaco.club/