【統計一口メモ　第27話】2因子分散分析って？
―その１．質的解析―

名古屋市立大学大学院医学研究科 非常勤講師　薬学博士　松本一彦

「分散分析（ANOVA：Analysis of Variance）を分散の検定だからバラツキをみる　検定法だと思っていませんか？　分散分析といっても、“母平均の検定”です１）。

因子が1種類（A）であるようなデータ形式を１因子分散分析（One way ANOVA：一元配置分散分析）とよび、2種類（A, B）あるものを2因子分散分析（Two way ANOVA：二元配置分散分析）とよびます。ここでは、1因子分散分析として雌雄別々に解析したときと、雌雄を合わせて（単に足すのではなく、因子としてとりあげます）解析したときの違いを見てみましょう。

§１．1因子分散分析（雌雄別）

雄ラット1群4匹で4薬剤の生理活性値を調べた。薬剤間に差があるだろうか？

検定はF検定を用いる。片側検定でF分布の上側確率だけを調べればよい2）。

帰無仮説：H0=μ1=μ2=---=μa

対立仮説：H1＝少なくとも１つは≠

F比＝水準間平均平方／残差平均平方＝0.562/0.225＝2.497

p＝FDST(2.497,3,12)＝0.1095

結果：雄ラットでは薬剤間で差は見られない。

雌ラット

結果：雌ラットも薬剤間で差は見られない。

§２．1因子分散分析（雌雄足し算）

分散分析表

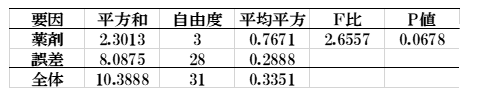
結果：雌雄を足してN数を増やした分ｐ値は0.067と小さくなりましたが、有意差は見られません。

§３．2因子分散分析

1因子分散分析では雌雄別と雌雄を足し算して検定をしましたが、いずれも有意差はみられません。そこで、「雌雄」を因子としてとりあげた解析をしてみます。

使用するデータは1因子分散分析と同じものですが、「雌雄」と「薬剤」の2因子で作表します。

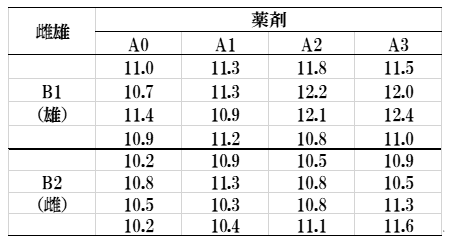
その分散分析表は次のようになります。

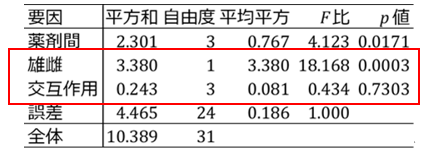
雌雄別の1因子分散分析と比べると、要因として「雌雄」と「交互作用」が加わっています。

それでは、分散分析表がどのように作られたのかを見ていきましょう。

①平均値表（4例の平均を求めます）

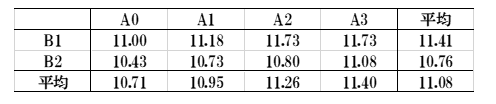
②残差表

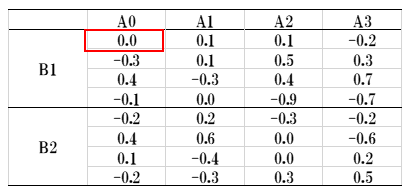
残差=観測値－平均値　(11.0-11.00=0.0)

③主効果と交互作用

主効果は水準の平均から総平均を引いた値。

B1の主効果＝11.41-11.08＝0.33

交互作用は平均から総平均とそれぞれの主効果を引いた値。

A0B1の交互作用＝11.00-11.08-0.33-(-0.37)=-0.04

④分散分析表

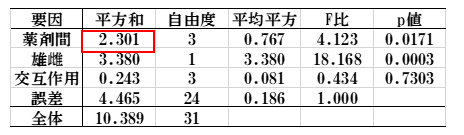
平方和の計算薬剤間＝2.301の場合：③表の主効果の値から

＝((-0.37)2＋(-0.13)2＋(0.18)2＋(0.32)2) x 8＝2.301

結論：薬剤間および雌雄間に有意差がみられた（p=0.017, ｐ＜0.001）。「雌雄ｘ薬剤」の交互作用が有意でなかったことから、薬剤間比較で雌雄の影響はないといえる(ｐ=0.730)。

2因子分散分析で雌雄を因子として捉えた場合、誤差が交互作用と雌雄の分だけ小さくなります。そのためにｐ値が小さくなり有意となりやすくなります。探索的な研究の場合にはこのように、雌雄の結果を見てから雌雄を因子として合わせた解析も許されるものと思われます。

※ボクのつぶやき：2因子分散分析で有意差がみられても、どことどこの群間に差があるんだろう？ということは教えてくれないなー。そのときは、また“2群間の差の検定”をやるわけだけど、やっぱ、この検定は、“差がない”ことを知りたい場合の方が使い勝手がいいのかも。

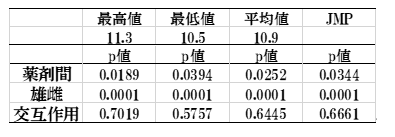
§４．欠測値があったとき

雌雄データでA3群の雌の値（B2A3＝11.6）が欠測値だったとします。理論的に欠測値を補う方法はありますが、探索的に検討する場合は便宜的にその群の平均値を使うことがあります。今回の例では、欠測値を「雌 ｘＡ３群」の最高値(11.3)、最低値(10.5) 、平均値(10.9)で補った場合にｐ値は次のようになりました。ＪＭＰソフトは欠測値があっても計算してくれるので、その値と比較してみました。その結果やはり平均値がJMPの値と近似していることがわかりました。

• 1）松原望「統計の考えかた」放送大学教材（放送大学教育振興会）2000年
• 2）芳賀敏郎「医薬品開発のための統計解析第2部実験計画法」サイエンティスト社2014年