【統計一口メモ 第28話】2因子分散分析って?
―その2.量的解析―
名古屋市立大学大学院医学研究科 非常勤講師 薬学博士 松本一彦
§1.質的解析
前回の第27話では、2因子分散分析の“質的解析”をとりあげました。今回はその“量的解析”について解説します。質的と量的って何が違うのでしょうか?下記の表を比べてみましょう。
表1 質的解析
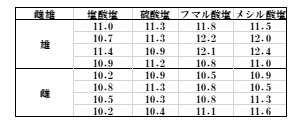
表2 量的解析
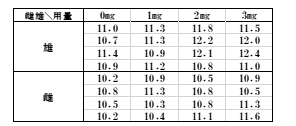
データは全く同じですが、質的は薬剤(塩の種類)、量的は投与量になっています。
質的解析の分散分析表は次のようになります。
表3
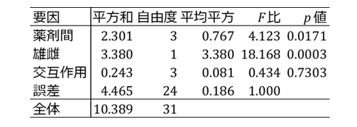
結果は薬剤間と雌雄間に差がみられるものの、交互作用に有意差が見られていないことから、雌雄が薬剤間の差に影響していないことを示しています。
さて、量的解析ではどのようになるのでしょう。
§2.量的解析―雌雄別々―
はじめに、雌雄それぞれで量的解析をやってみましょう。
質的(雌雄)に対し、投与量を水準にとった量的解析を行います。雄をB1、雌をB2と略します。まず雌雄それぞれで水準ごとに平均値を求めます。なお、表にある赤枠は後の残差を計算するときの数値で使います。
表4
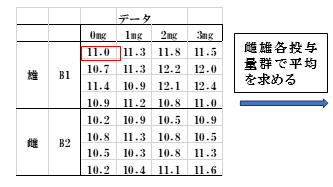
表5
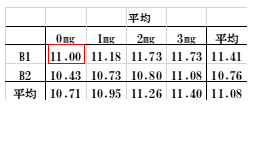
表6
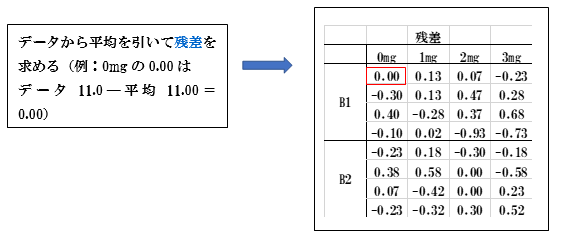
残差の平方和は0.002+(-0.30)2+―――+0.522=4.465で純粋誤差(誤差)として§3.の「雌雄共通傾きのモデル」の分散分析表に表示されます。
量的因子の各要因における平方和はエクセル関数のLINEST関数を使って計算します。
手法はやや複雑なのでここでは述べませんが、詳しくはグリーン本第1部p2341)を参照してください。
まず、雌雄それぞれで解析します。下図は横軸に投与量を縦軸に測定値をとった雌雄比較図です。
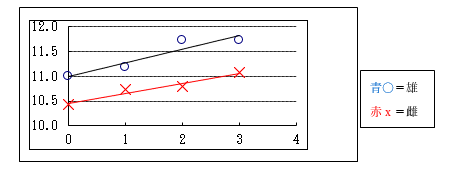
表7の雄にはLINEST関数で得られた出力項目の説明語を日本語で、表8の雌はその略号を左側にまとめて示しています。これらの解析結果の一部を分散分析表に使います。
表7
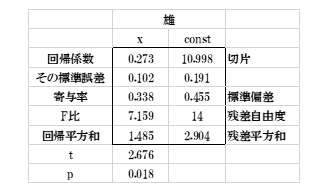
表8
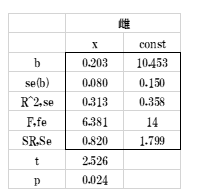
ここで回帰係数の行で、xの0.273は傾き、Const10.998は切片を表します。3行目の標準偏差0.455は「誤差の標準偏差」ですが、分散分析表には現れません。回帰係数は直線の傾きを表します。すなわち、薬効の強さを表すので、雄の0.273は雌の0.203より大きく薬効が強いことを示しています。しかし、その強さの程度(差)は傾きの違いからだけではわかりません。傾きが同じにした時にその差の程度がわかります。そのためには、傾きを共通にした解析(§3)を行います。さらに、ここではt統計量とp値が示されています。このp値は回帰係数0.273の有意性の検定です。回帰直線とみなしていいかどうかを検定しています。雄の場合p=0.018で有意となりました。
分散分析表は次のようになります。
表9 雌雄別分散分析表

ここで、質的解析では出てこなかったLOFについて説明します。
LOFはLack Of Fit(あてはまりの悪さ)のことで、各水準の平均点が回帰直線からどのくらい離れているか、すなわち、直線があてはまっているかどうかを判断するための量のことです。雌雄ともLOFが有意でない(p>0.05)ことから“あてはまりは良い=直線と認められる”ことがわかります。
§3.量的解析―雌雄傾き共通とするモデル―
雄を基準として雌がどれだけ違うかを見ます。それには雌を0、雄を1としたダミー変数を使い、変数名を「雌」とします。
表10
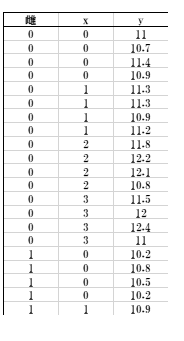
表11のLINEST関数表に示されているconst(切片)11.05は、雌雄の傾きを共通とすると切片は雄が11.05のときに雌はその差が-0.650という意味です。
すなわち切片は10.400となります。
表11
回帰式は ymale=0.238x + 11.05,
yfemale=0.238x + 10.40 となります。
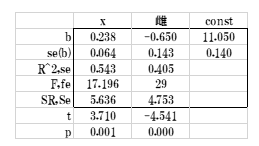
ここで投与量x(左)、雌雄(右)のLINEST関数表は次のようになります。
表12
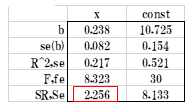
表13
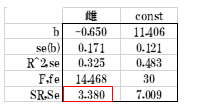
投与量xの平方和SRは2.256、雌雄の平方和SRは3.380で合計が下の投与量と雌雄を考慮したLINEST関数表の回帰の平方和5.636になります。でも,この数値は分散分析表には 反映されません。
表14 投与量と雌雄を考慮したLINEST関数表
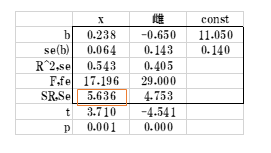
表15 傾斜を共通とする分散分析表
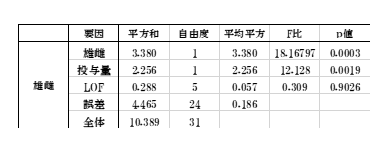
雌雄と投与量の平方和(3.380、2.256)は先のLINEST関数表(表12、13)の回帰平方和SRから導きます。LOFは表14の残差の平方和4.753からこの分散分析表(表15)の誤差4.465を引いた値になります、
自由度は雌雄、投与量とも1になります。投与量の水準数には関係ありません。質的解析とは異なるので注意が必要です。LOFの自由度5は本来ならば次の§4で示すように量的解析には交互作用が入りますが、傾斜が共通ということで省かれています。 交互作用の分も含めて水準4に1がプラスされ5となります。
※ボクのつぶやき:量的解析の自由度って理屈で考えても分かりにくいなー。投与量の場合は数ではなく、回帰の自由度が2だから、雌雄と投与量で分けることになるといわれるのだけど。
§4.量的解析―傾きが異なるモデル―
共分散分析は傾きが共通であることが前提になります。この2因子分散分析の量的解析にはその前提はありません。また、先の傾きが共通の分散分析に交互作用が加わることが 異なります。分散分析表の作成方法とその読み方について説明します。
表16 傾斜が異なるときの分散分析表
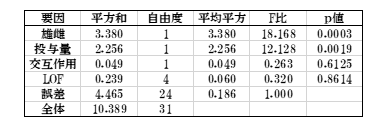
先にも述べたように傾斜が共通のときの分散分析表との違いは、交互作用の有無です。 交互作用は「投与量x雌雄」でこれが有意でないということは、投与量の傾きには雌雄は 関係していないことを表しています。反対に有意であると雌雄で差があることになります。雌雄を一緒に解析したい場合は雌雄間に差がないことが必要になります。交互作用の平方和は表7、8の雌雄別々に見た投与量の回帰平方和1.485と0.820の合計2.305と表15の傾きを共通としたときの投与量の回帰平方和2.256の差0.049を求めます。LOFの値は同じ表7、8の残差平方和2.904と1.799の合計4.703と繰り返し誤差=誤差4.465の差0.239を求めます。自由度は交互作用が1、LOFは投与量の水準数4となります。
以上で分散分析表の説明を終わりますが、実務で使用するときに最も注目するのはやはり投与量のp値で今回はp=0.0019と有意でした。雌雄差は当然あると思っていたのですが、交互作用がp=0.615で有意でないことから、投与量の傾きに雌雄で差はないことがわかります。芳賀先生はグリーン本1)で「傾斜が異なるときの分散分析表(表16)で交互作用もLOFも有意でないときは、これらを誤差に含めて解析することもありだけど、それは繰り返しn数が少ないとき、すなわち誤差の自由度が少ないときに限定すべき」と述べています。
※ボクのつぶやき:交互作用とLOFの値が小さいときに誤差に含めて誤差の自由度を大きくするとp値が小さくなる可能性が高くなるので、生物統計をやる実務者にはうれしい情報だけどルーチン的にはやらないなー。
§5.Pharmaco ANOVAでやってみよう
これまでの解析をエクセルでやっていく人は、まずいませんね。
きっと市販のソフトを使われると思います。市販ソフトはそれぞれ制作者の考えがあり、必ずしも同じ結果が得られるとは限りません。それでも、解析結果が実務に支障をきたさなければ「まっ、いっか」と考えるゆとりも必要なようです。
自分の使っているソフトを信じるしかないのが実務者の統計解析への向き合い方なんでしょう。
表17 Pharmaco入力形
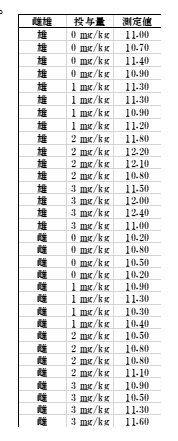
さて、例題の解析をPharmaco ANOVAでやるとまず、右の表のような入力形式に整えます。解析結果は次のようになります。
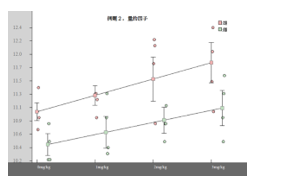
表18 分散分析表
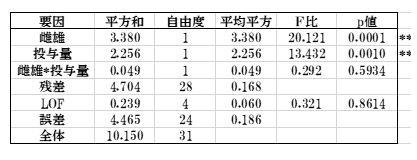
ここでは交互作用は「雌雄*投与量」と表示されます。またグリーン本にはない「残差」が表示されています。それは、PharmacoのF比の検出方法をJMPに合わせたことによります。JMPの結果とグリーン本ではF比とp値が異なります。
表19
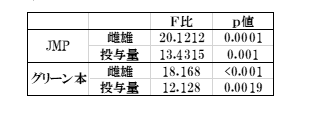
グリーン本では「純粋誤差(誤差)」を分母としてF比を求めているのに対して、JMPでは「純粋誤差+LOF」をF比の分母としているためです。Pharmacoではこれを「残差」として表し、JMPと同じにしました。
- 1)芳賀敏郎「医薬品開発のための統計解析」第2部 サイエンティスト社 2014年
- Pharmaco ANOVAソフトはUSB版がサイエンティスト社info@scientist-press.com ダウンロード版がPharmaco工房のホームページhttps://pharmaco.club/から購入できます。








 Today:
Today:


