【統計一口メモ　第30話】乱塊法って何？一般線形モデルって？

名古屋市立大学大学院医学研究科 非常勤講師　薬学博士　松本一彦

表１　データと平均、効果

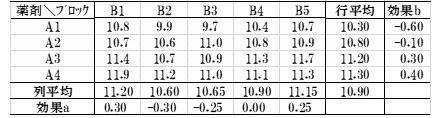
芳賀敏郎「医薬品解析のための統計解析第2部」^１）よりデータ引用

本試験は、行でみると薬剤を因子とする試験で、列でみるとケージの位置（ブロック）を因子とする試験です。１ケージ4匹のラットに、各薬剤をそれぞれ1匹ずつ投与し、5ケージで２０匹の試験となります。本試験は薬剤を比較するのが目的であり、ケージの位置は実験の誤差を小さくするために取り上げた因子です。このように比較目的ではない因子をブロック因子と呼び、薬剤のように比較目的の因子を制御因子と呼びます。

このようなブロック因子を用いる解析が乱塊法（Randomized block design）です。２因子分散分析実験とは異なり、ブロック内の例数が１で反復測定を行っていないため、交互作用は求まりません。

系統的な誤差が含まれることが予想されるとき（この場合はケージの位置）、それをブロック因子として実験を計画すると、系統的誤差が小さくなり、検出力を高めることができます^１）。

§１．乱塊法―質的データ

薬剤A1からA4のような質的なデータで分散分析表作成の手順を見てみましょう。

手順１：まず、表1の「効果a,b」を原表の薬剤とブロックそれぞれの「平均値－総平均」で求める。例えばB1の効果0.30は、B1の平均値11.20－総平均10.90、A1の効果-6.0はA1の平均値10.3－総平均10.90から求める。

手順２：表２に観測値と(総平均＋効果a＋効果b)の差を「残差」として求める。例えば、A1×B1の0.20は10.8－｛10.9＋0.30＋(-0.60)｝で求める。

表２．残差

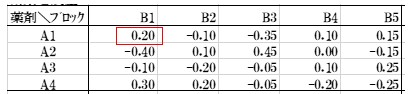
手順３：薬剤４種とブロック５を水準数として表示する。

手順４：薬剤、ブロック、残差の平方和を求める。

１．薬剤平方和：効果aの平方和の合計にＢの水準数５を掛ける。
｛ 0.60²＋(-0.10)²＋0.30²＋0.40² ｝×５＝3.100

２．ブロック平方和：効果bの平方和の合計にAの水準数４を掛ける。
｛ 0.30²＋(-0.30)²＋(-0.25)²＋0.00²＋0.25² ｝×4 ＝1.220

３．残差平方和：0.20²＋---＋(-0.25)²＝0.960

４．全体（総平方和）：原表の偏差（観測値－総平均）の平方和
(10.8－10.9)²＋---＋(11.3－10.9)²＝5.28

手順５：自由度は、全体：20－1＝19、薬剤：4－1=3、ブロック：5-1=4、残差：全体－(薬剤＋ブロック)＝19－(3＋4)＝12、

手順６：分散分析表を作成する。
平均平方は平方和／自由度、F比は薬剤、ブロックの平均平方を残差平方和との比で求める。p値はエクセル関数FDIST(F値、薬剤自由度、残差自由度)で求める。

表３．分散分析表（乱塊法）

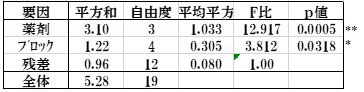
結果：薬剤間とブロックで有意差がみられた。

§２．データに欠測値がある場合

表４．データと平均値

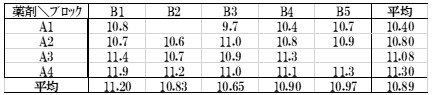
分散分析表は次のようになります。

表５．欠測値がある場合の分散分析表

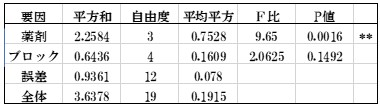
表５．欠測値がある場合の分散分析表

結果:薬剤間に有意差がみられたがブロック間には有意差はみられない。

解説：欠測値がA1群×B2群とA3群×B5群にそれぞれ1例みられたデータでは欠測値がない場合と比べて「薬剤」のp値が0.0005から0.0016と大きくなりました。なお、ブロックは0.0318から0.1492となり有意差がみられなくなりました。

JMPは欠測値がある場合には最小二乗平均を用いて解析しています。その値は薬剤が0.0039でブロックが0.1080であり、エクセル解析と若干異なった結果を示しています。

３．量的解析

表１のデータで薬剤が0㎎／㎏～30㎎／㎏の量的になったときを表６に示します。

表６

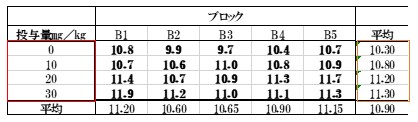
モデル式はy_ij＝(b0+b_ix_i)＋c_j＋e_ij

＝ｙhat_i＋（ｙbar._j－ｙbar..）＋（ｙ_ij－（ｙhat_i＋ｃ_j))

表6の投与量と平均値を用いて、LINEST関数で回帰式を求めます。

表７．

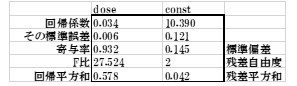
回帰式ｙ＝0.034ｘ＋10.390

表８．

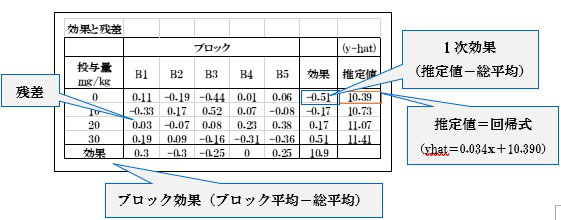
ブロックの効果は表１と同じで、「ブロック平均－総平均」で求める。一方、投与量の効果は推定値ｙhatを使います。yhatは回帰式b１X＋ｂ０から計算します。yhat＝0.034x＋10.390で０mg／kgのときはと10.39となります。それは表８の推定値の一番上に求められています。30mg/kgは11.41となります。推定値の効果は「推定値―総平均」から求める。0㎎／㎏の場合は10.39－10.90＝10.39-0.51となります。

分散分析表を作成するためには、各因子で平方和を求めます。

１．総平方和＝S_Tは表6の観測値でDEVSQ関数から5.28、自由度は19です。

２．水準間平方和＝S_Aは表６の投与量を水準とした平均値のDEVSQ関数から3.10、自由度は３です。

３．回帰平方和＝1次＝S_Rは投与量の効果でSUMSQ関数から2.89、自由度は１です。

４．LOF（Lack of fit＝あてはまりの悪さ）平方和＝S_LOFで平均値と推定値のずれを表しています。水準間平方和3.10－回帰平方和2.89＝0.21として求める。自由度は3－1＝2です。

５．ブロック平方和＝SBは表８のブロック効果でSUMSQ関数から1.22、自由度は４です。

６．残差平方和＝Seは表８の残差でSUMSQ関数から0.96、自由度は19－7＝12です。

表９．分散分析表

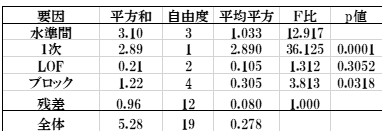
結果は投与量（1次）に有意差がみられており、LOFに有意差がないことから、投与量に伴った有効性であるといえる。

※ボクのつぶやき：乱塊法ではブロック因子は解析対象に入れないことになっているようだけど、ブロックの違いも考察には大事な気がする。ちなみにJMPはLOFの計算はせずに、ブロックごとの解析を行っている。

§４．フリードマン（Friedman）検定―ノンパラメトリック乱塊法

同じデータを使ってその方法を眺めてみよう。

データと平均

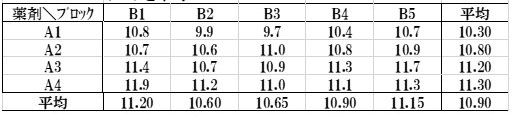
手順１．ブロックごとに小さい順から順位をつけてその平均をとる。同値は順位の平均。
クラスカルワリス検定のように全体を通して順位をつけるのではないことに注意。

表10．データと平均

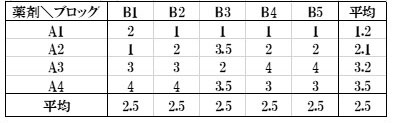
手順２．効果と残差を求める。効果は総平均―群平均でブロックの効果は０となる。

A1の効果-1.30＝1.2－2.5、A1×B1の残差0.80＝2－(-1.30＋2.50)となる。

表11．効果と残差

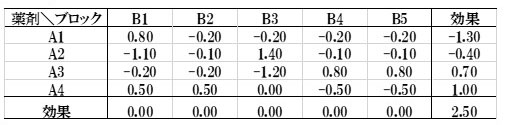
手順３．分散分析表を作成する。

１．薬剤平方和は薬剤の効果からSUMSQ関数×５で16.7を求める。

２．残差平方和は残差からSUMSQ関数で7.8を求める。

３．総平方和（全体）は表10の順位に変換したデータからDEVSQ関数で24.5を求める。

表12. 分散分析表

結論：薬剤間で有意差（P＝0.0168)がみられた。

※パラメトリックの乱塊法との違いは

１）「F比」が「カイ二乗（χ²）」に変っている。

２）ブロック間の検定を行わないため、全体の自由度を「薬剤」と「残差」の

自由度の和にする。なお、JMPはFriedman検定に対応していない。

§５．乱塊法解析の意義

A.Grafen, R.Hailsは著書^2）の中で次のように述べています。

実験計画の３つの基本概念はFisherの３原則と呼ばれる。

１．反復（replication) ２．無作為化(randomization)３．ブロック化（blocking)

・データのもつ変動は、解析対象の説明変数の変動と誤差変動に分解される。

・誤差変動が小さくなると、その実験の検出力は高くなる。

・ブロック化はその誤差変動を小さくするために考案された実験計画の手法である。

・ブロック化を利用すると、解析の精度が上がり、有意な結果を発見しやすくなる。

・ブロック内ではどの区画も同質にし、ブロック間ではできるだけ違うようにする。

※ボクのつぶやき：Grafenは、「ブロック間はできるだけ違うようにする」というけど、実務者は、なるべくブロック間も同じようにして、誤差変動を少なくするように心がけるもの。それでも、予期せぬことから他のブロックと異なるものが入り込むことがあり、そのため、解析結果に疑問を残すのでは？Pharmacoソフト（Pharmaco ANOVA）^3）はそのような場合にブロックでの解析ができるようにしたのだけど。

§６．Pharmaco ANOVAソフト^3）と一般線形モデル解析（GLM）^＊

乱塊法は教科書には、よくとり上げられていますが、論文ではあまり見かけない馴染みの薄い手法といえます。一方、A.Grafen、R.HsilisはGLMの解法例として、次の例題でとりあげています。

＊GLMは一般線形モデル（general linear model）と一般化線形モデル（generalized linear model）両方の略語として用いられます。

表13．斑点個数データ表

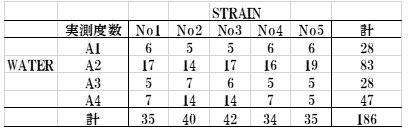
斑点の個数のようなデータはポアソン分布すると言われています。このデータをカテゴリカルデータとして分割表で解析するとPharmacoもGLMもp値が0.7981で斑点の出現に4種のWATER間で有意差はみられません。

表14．分割表結果

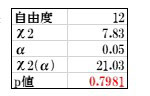
このデータをポアソン分布データとしてGLMで解析した結果は、Pharmacoの乱塊法で解析した結果と全く同じで、WATER間に有意差がみられました。

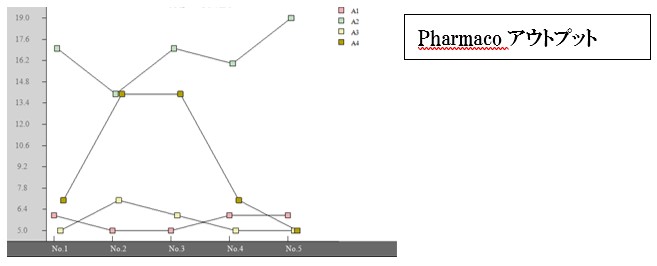
表15．

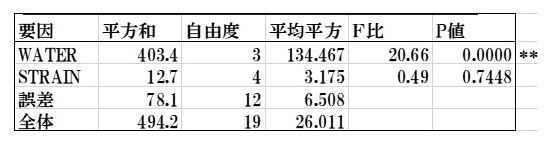
乱塊法ではSTRAINをブロックとしてとりあげて、WATER間の違いを検定した形になります。

一般線形モデルは正規分布にこだわらずに解析するという実務者には有用な手法なのですが、Rなどのソフトを使いこなすのに時間がかかりそうです。

• 1）芳賀敏郎「医薬品開発のための統計解析第2部サイエンテイスト社2004年
• 2）A.Grafen, R.Hails:一般線形モデルによる生物科学のための現代統計学共立出版2014年
• 3）Pharmaco工房：https://pharmaco.club/