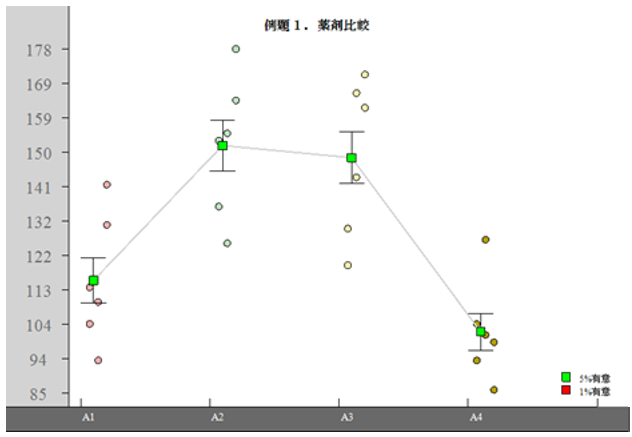
【統計一口メモ 第31話】枝分かれ実験って?
名古屋市立大学大学院医学研究科 非常勤講師 薬学博士 松本一彦
基礎試験、臨床試験ともに測定を2回とか3回実施して、試験の精度を高めることは、しばしば行います。でも、試験動物がイヌの場合とマウスやラットの場合では、使える例数により、検定方法が変わることがあります。今回のメモは、その違いについての話題です。

表1 イヌ試験
繰り返しのある2因子実験
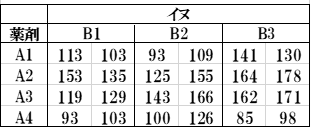
表2 マウス試験
枝分かれ実験

測定回数が2回という同じデータでも、表1のようにイヌ3頭の実験と表2のようにマウス12匹の実験では解析法が異なります。今回は後者の「枝分れ実験」について解説します。
§1.エクセルでの解析
芳賀敏郎先生は著書1)の中で「薬剤3種に対し各薬剤3匹で、1匹のマウスで3回検査するような実験を枝分れ実験(Nested Design)という。ここでは、個体差と測定誤差の両方を考慮して、実験の効率を高くすることを目指している」と書かれています。
図1
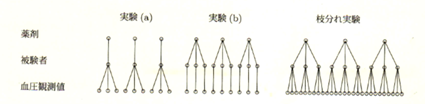
図1は枝分かれ実験と他2つの実験の比較を示しています。
実験(a)は、被験者3人で、それぞれ繰り返し測定が3回のケースです。1薬剤に被験者1人なので、有意差があっても被験者間か薬剤間かの違いはわかりません。
実験(b)は、繰り返しがないケースです。測定回数は実験(a)と同じ9回でも被験者は(a)の3倍、9人が必要となります。結果が有意差を示せば、薬剤間に優劣があると結論できますが、測定回数は1回なので測定誤差が心配です。
枝分れ実験は3つの薬剤にそれぞれ3例の被験者があり、さらに3回の測定を行うという構成になっています。これならば、結果が有意差を示せば、薬剤間に差があると言えます。
それでは、例題にしたがって動物実験例で解説していきます。
§2.「枝分れ実験」エクセル解
表3 表4 表5
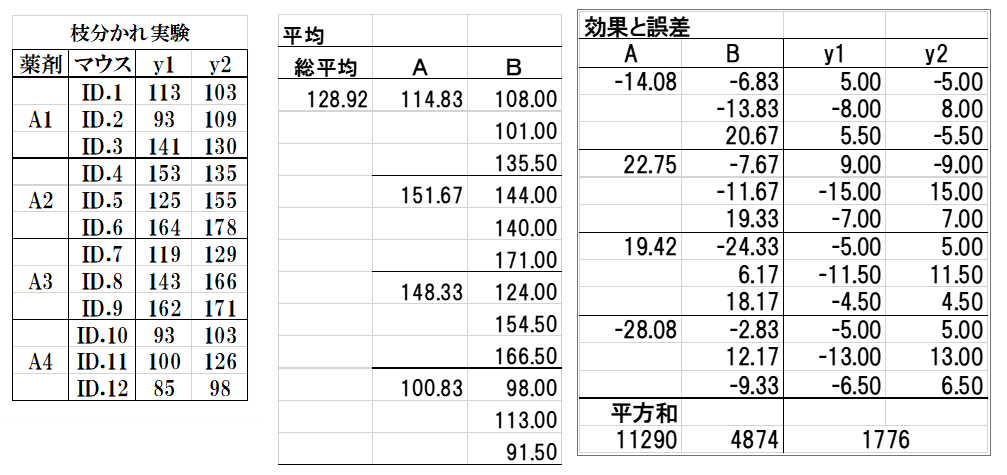
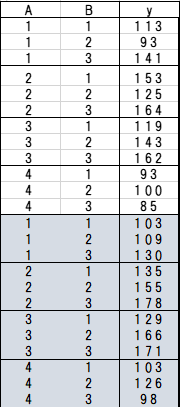
手順1.表3のID.1のy1とy2の平均値108.00を求める。同様に、ID.2~ID.12の平均値を求める(表4のB列)。
手順2.A1の3つの平均値A1=114.83を求める。同様に、A2~A4の平均値を求める(表4のA列)。
手順3.A1~A4の総平均値128.92を求める(表4の総平均)。
手順4.薬剤A1の平均値114.83から総平均値128.92を引いて-14.08を求める。これを”効果“という。同様に、A2~A4の効果を求める(表5のA列)。
手順5.ID.1の平均値108.0から薬剤Aの平均値114.83を引いて-6.83を求める。同様に、ID.2~ID.12の効果を求める(表5のB列)。
手順6.ID.1の観測値113(y1)からその平均値108.0を引いて5.00を求める。これを“誤差”という。同様に、ID.2~ID.12の誤差を求める(表5のy1列、y2列)。
手順7.薬剤Aの平方和SAは表5のA列の平方和に薬剤数4と薬剤毎の動物数3を掛けて求める。
Σ{(-14.08) 2 +---+(-28.08) 2 } × 4 × 3 = 11290
手順8.動物間Bの平方和SB(A)はAの水準ごとのBの水準間の平方和という意味で表5のB列の平方和に繰り返し数2を掛けて求める。
Σ{(-6.83) 2 +----+(-9.33) 2 }× 2 = 4874
手順9.誤差の平方和Seは表5のy1列、y2列の平方和で求める。
Σ( 5.002 2 +----+ 6.5092 2 )= 1776
手順10.SAの自由度は 4-1=3
SB(A)の自由度は 4×(3-1)=8
Seの自由度は 4×3×(2-1)=12となる。
手順11.分散分析表を作成する。
表6 分散分析表

B(A):(被験動物)のF比を計算する分母は、残差の平均平方(Ve)148.00を用いる。
※F比欄の1.000は比較する要因の分母になる平均平方を示しています。
A: 薬剤間のF比を計算する分母は、残差のVeではなく被験動物のVB(A)609.29を用いる。それは、同じ薬剤を投与された被験動物間のバラツキに比べて、薬剤間の違いが大きいかどうかを見ることによる。
※このF比の求め方がイヌの例題の「繰り返しのある2因子分散分析」と異なることに注意です。
p値0.018はFDIST関数FDIST(F比、自由度1、自由度2=6.176、3、8)で求める。
F.DIST関数の場合は(F比、自由度1、自由度2、FALSE)で求める。
結論:p=0.018で薬剤間に有意差がみられる。
※ボクのつぶやき:分散分析の宿命ではあるけど、有意差がみられたからって、どことどこの差なのかは教えてくれない。下記の図をみて、さらなる群選択をするか、2回の平均で多重比較をしてから4薬剤の優劣をみるのもいいけど、どの薬剤を選択すべきかは、図からくみ取ることができる気がするなー。
§3.JMPでの解析
JMPでは入力形式に要注意です。マウス12匹を4薬剤に配置するときに、表7のように薬剤毎に1,2,3としなければなりません。1から12までの番号をふらないということです。そして2回の測定を上下に並べます。
表7
結果のアウトプットの一部は表8のようになります。
表8

§4.Pharmacoでの解析
Pharmacoの入力形式もJMPと同じ1薬剤3例です。ただし、2つの測定値は横に並べます。
表9

Pharmacoのアウトプットは下記のようになります。結果はJMPと同じです。
表10 分散分析表

§5.スネデカー・コクランの例
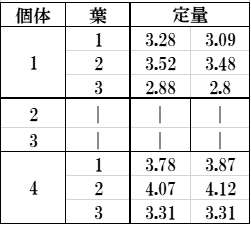
スネデカー・コクラン2)は、「標本内の標本、枝分れ分類」の節でつぎのような例を挙げています。「4個体が無作為にとられ、各個体から3枚の葉が無作為にえらばれた。各葉から100mgの試料が2つとられ、それらについて微量化学的方法でカルシウムが定量された。この直接の目的は、植物個体、同じ個体の葉、同じ葉についての定量という3つの変動因による平方和を分離することである」。この植物個体を水準差、個体の葉を個体差、
葉の定量を測定誤差と呼び変えると今回の例題と同じになります。
表11 かぶら葉
-
1)芳賀敏郎「医薬品開発のための統計解析」第2部 サイエンティス社 2014年
-
2)スネデカー・コクラン「統計的方法 第6版」岩波書店 1977年